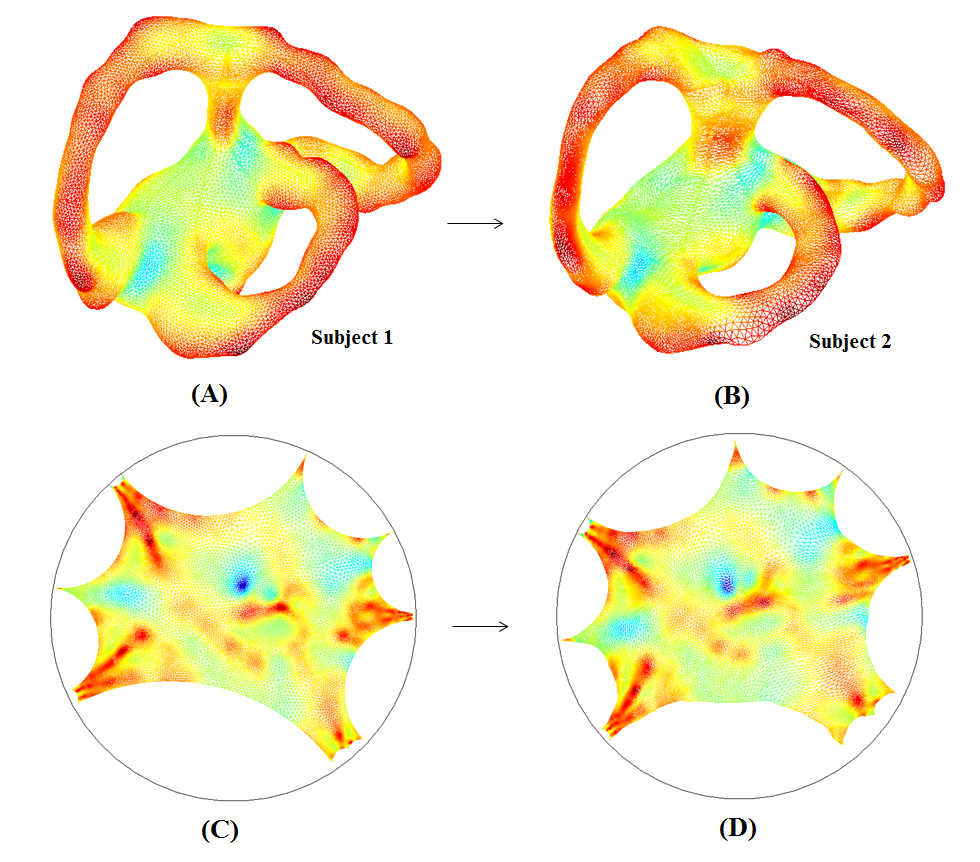
Geomtric registration of high-genus surfaces
Project Description:
This paper presents a method to obtain geometric
registrations between high-genus ($g\geq 1$) surfaces. Surface registration
between simple surfaces, such as simply-connected open surfaces, has been well
studied. However, very few works have been carried out for the registration of
high-genus surfaces. The high-genus topology of the surface poses a great
challenge for surface registration. A possible approach is to partition surfaces
into simply-connected patches and registration can be done in a patch-by-patch
manner. Consistent cuts are required, which are usually difficult to obtain and
prone to error. In this work, we propose an effective way to obtain geometric
registration between high-genus surfaces without introducing consistent cuts.
The key idea is to conformally parameterize the surface into its universal
covering space, which is either the Euclidean plane or the hyperbolic disk
embedded in $\mathbb{R}^2$. Registration can then be done on the universal
covering space by iteratively minimizing a shape mismatching energy measuring
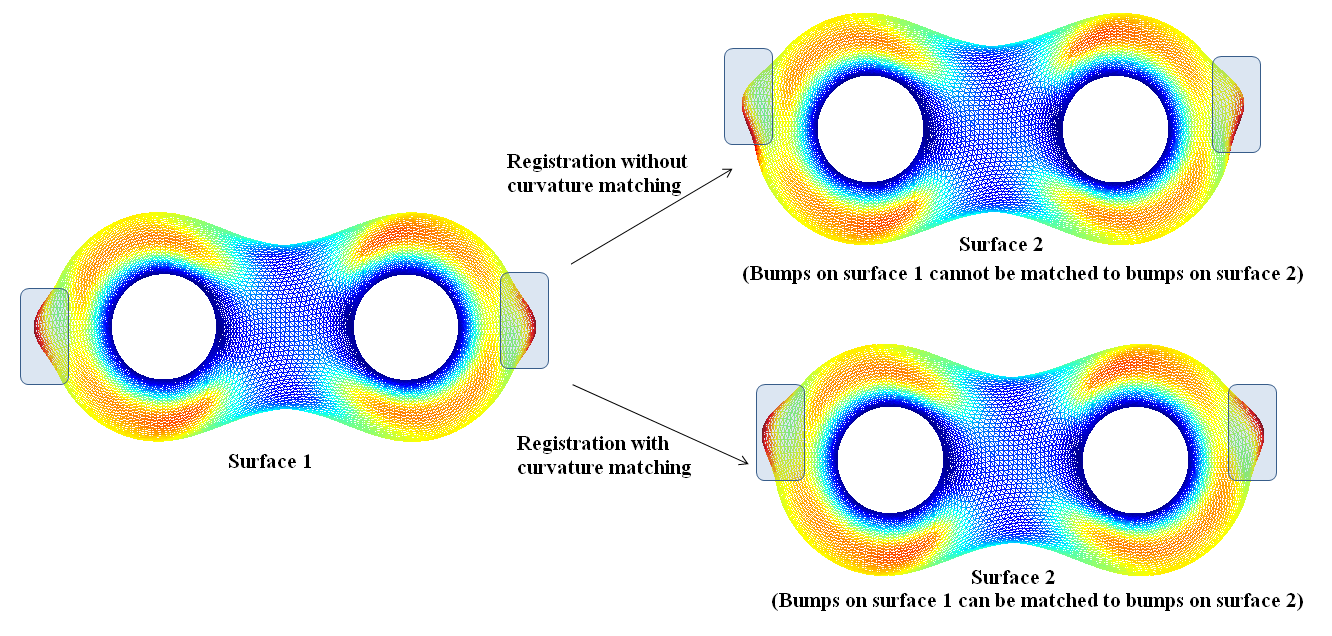
the geometric dissimilarity between the two surfaces. The Beltrami coefficient
of the mapping is considered and adjusted in order to control the bijectivity of
the mappings in each iterations. Our proposed algorithm effectively computes a
smooth registration between high-genus surfaces that matches geometric
information as much as possible. The algorithm can also be applied to find a
smooth registration minimizing any general energy functionals. Numerical
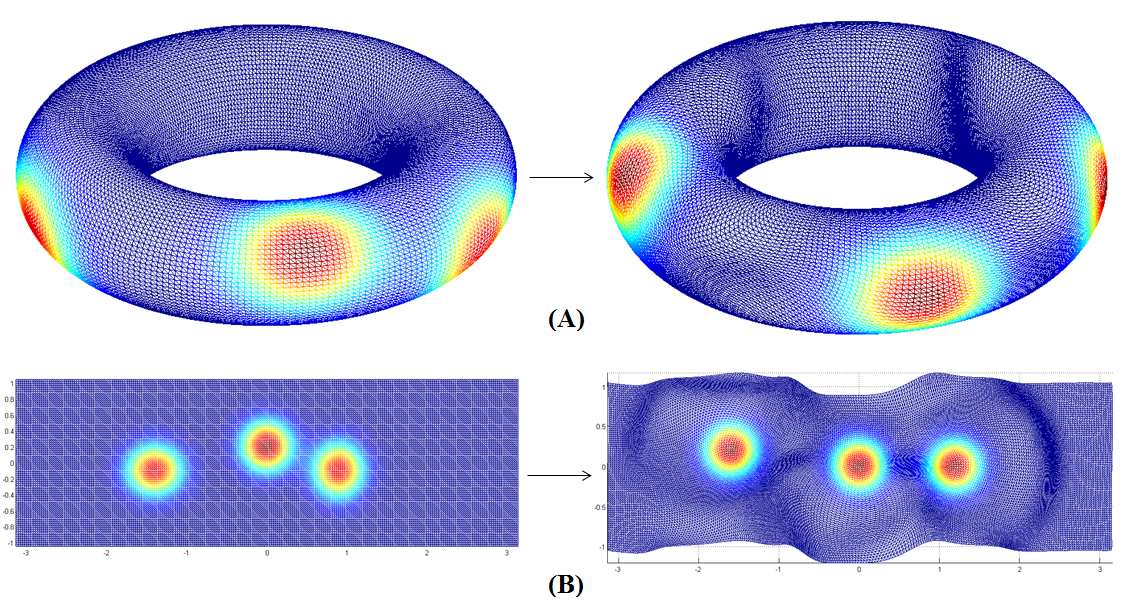
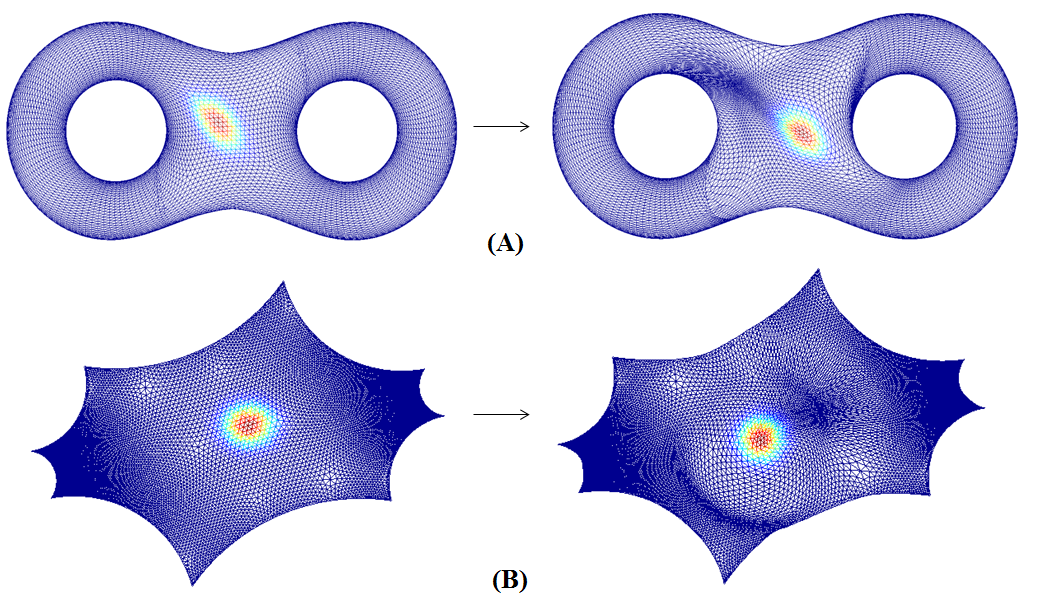
experiments on high-genus surface data show that our proposed method is
effective for registering high-genus surfaces with geometric matching. We also
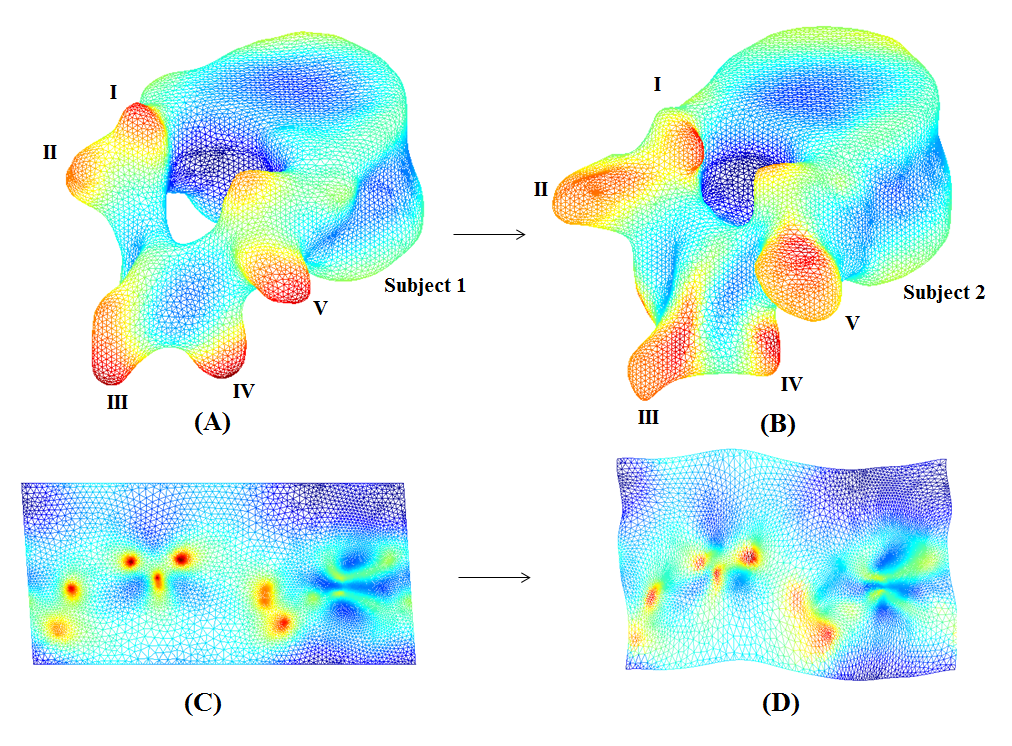
applied the method to register anatomical structures for medical imaging, which
demonstrates the usefulness of the proposed algorithm.
Publication:
- C.F. Wen, L.M. Lui, Geometric registration of high-genus surfaces, accepted, SIAM Journal on Imaging Sciences (2013)