Project Description:
Surface registration is widely used in machine vision and medical imaging, where 1-1 correspondences between surfaces are computed to study their variations. Surface maps are usually stored as the 3D coordinates each vertex is mapped to, which often requires lots of storage memory. This causes inconvenience in data transmission and data storage, especially when a large set of surfaces are analyzed.
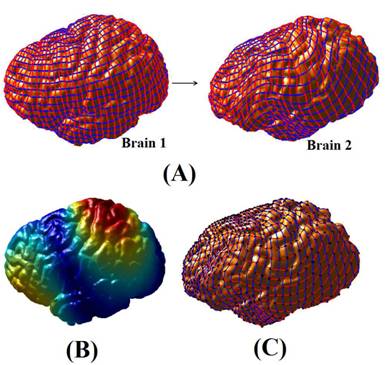
To tackle this problem, we propose a novel representation of surface diffeomorphisms using Beltrami coefficients which are complex-valued functions defined on surfaces with supreme norm less than 1. Fixing any 3 points on a pair of surfaces, there is a 1-1 correspondence between the set of surface diffeomorphisms between them and the set of Beltrami coefficients on the source domain. Hence, every
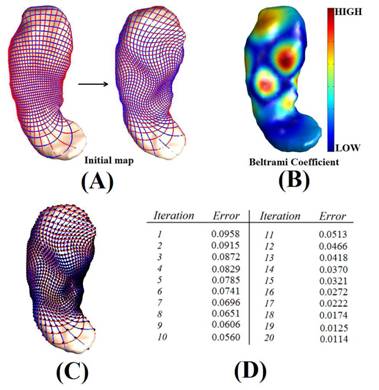
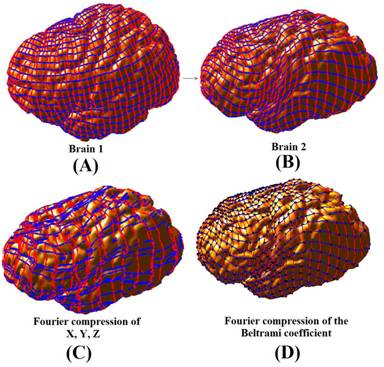
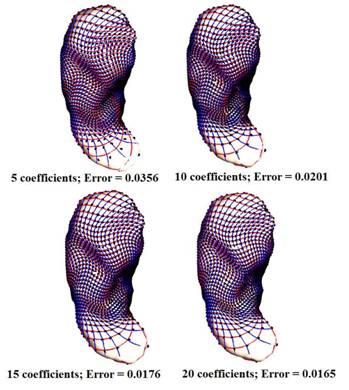
bijective surface map can be represented by a unique Beltrami coefficient. Conversely, given a Beltrami coefficient, we can reconstruct the unique surface map associated to it using the Beltrami Holomorphic flow (BHF) method introduced in this paper. Using this representation, 1/3 of the storage space is saved. We can further reduce the storage requirement by 90% by compressing the Beltrami coefficients using Fourier approximations. We test our algorithm on synthetic data, real human brain and hippocampal surfaces. Our results show high accuracy in the reconstructed data, while the amount of storage is greatly reduced. Our
approach is compared with the Fourier compression of the coordinate functions using the same amount of data. The latter approach often shows jaggy results and cannot guarantee to preserve diffeomorphisms.

Publication:

• Lok Ming Lui, Tsz Wai Wong, Xianfeng Gu, Tony Chan and Shing-Tung Yau, Compression of  Surface Registration using Beltrami coefficient, Computer Vision and Pattern Recognition (CVPR 2010), in press

Result: