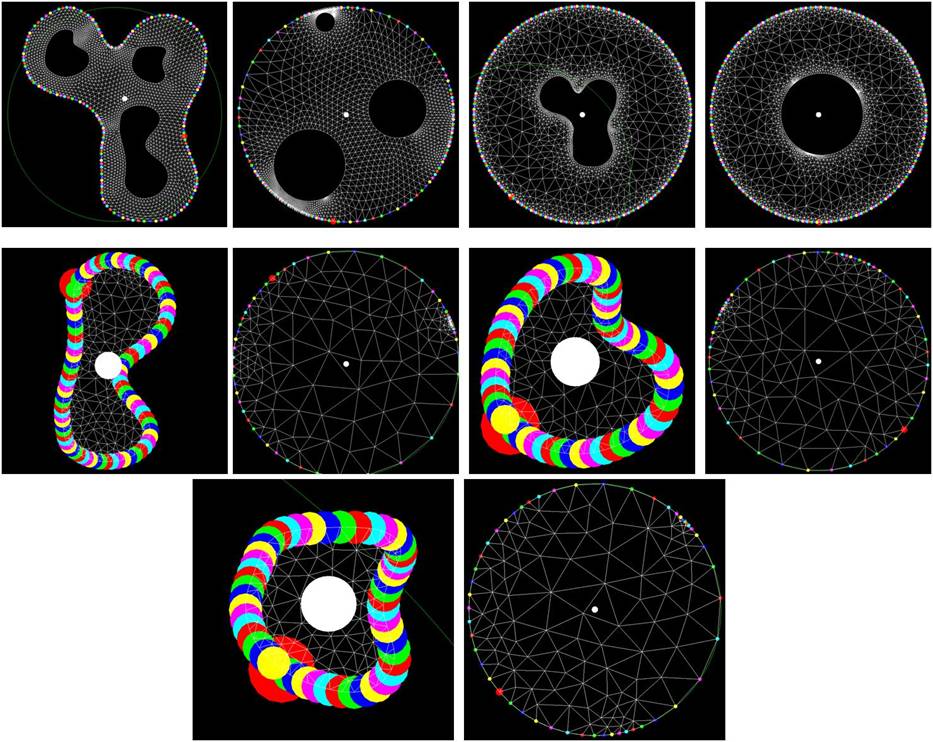
A Novel Shape signature of multiply-connected domain

Project Description:
The study of 2D shapes is a central problem in many different research areas, such as computer vision and medical imaging. In 2D shape analysis, classification and recognition of objects from their observed sihouette are extremely crucial and yet difficult. It usually involves a defintion of a metric on the 2D shape space, so that its mathematical structure can be used for further analysis. Although significant progress can be found for the study of 2D simply-connected shapes, none or very little works have been done on the study of 2D multiply-connected domains.  In this work, we proposed a representation of 2D multiply-connected domains using conformal geometry. 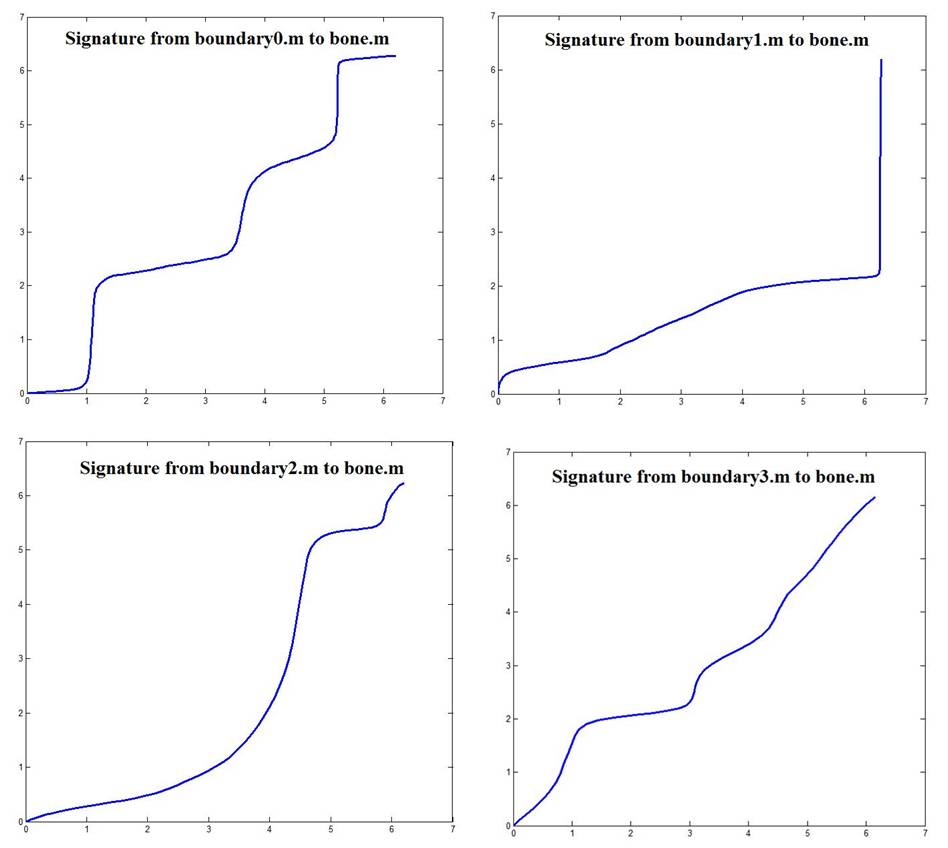A natural metric can be defined on the proposed representation space. Hence, a shape signature can be defined to measure the similarities between objects. This is done by mapping the exterior and interior of the object conformally to unit disks and punctual disks.  A set of diffeomorphisms from the unit disks to itself can be obtained, which are used to define shapes.  We prove mathematically that our proposed shape signature represents shape up to scaling and translation. Experimental results shows the effectiveness of our propsed method for 2D shape analysis.

Publication: 

• Lok Ming Lui, Xianfeng Gu, Shing-Tung Yau, A Novel Shape signature of multiply-connected domain, in preparation

Result: