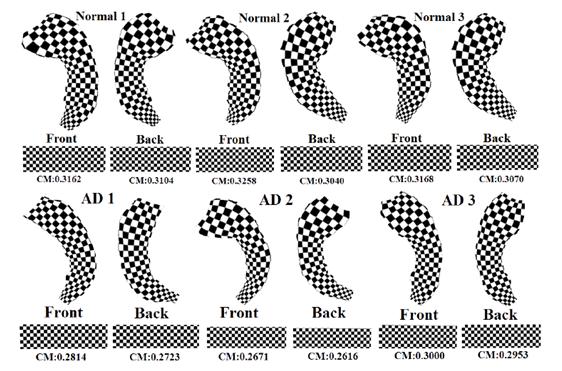
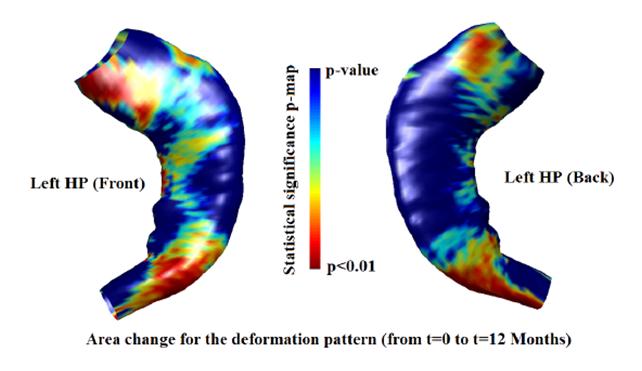
Instrinic feature extraction and Hippocampal Surface Registration using Harmonic eigenmap
Project Description:
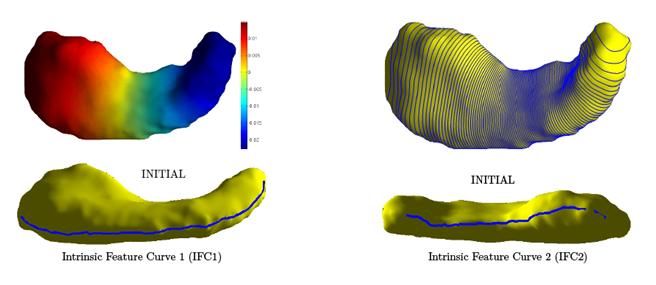
This work proposes a novel approach to extract two intrinsic feature
landmarks on hippocampal (HC) surfaces using their first non-trivial Laplace-Beltrami
(LB) eigenfunctions. These landmarks describe the global geometry of HC
surfaces and can potentially be used to define shape indices to study shape
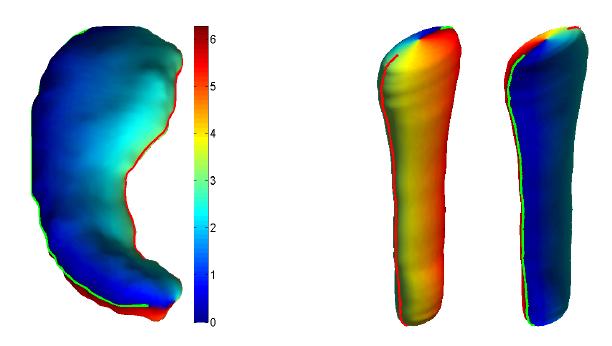
changes. We also propose a parametrization of HC surfaces called the eigen-harmonic
map (EHM), which maps
each HC surface onto a tubular domain and gives a longitudinal and azimuthal
coordinate to each surface. The longitudinal coordinate follows the same
direction as the eigenfunction. Each loop on the HC sur-
face with the same corresponds to a level-set of the eigenfunction (the
eigen-loop). The azimuthal coordinate takes a constant value along the longer
intrinsic landmark and minimizes the harmonic distortion of the map. Each
tubular domain is constructed according to the geometry of individual HC surface.
This gives a better parameter domain with much less geometric distortion compared
to the popular method of mapping HC surfaces onto spheres. With the EHM parametrizations,
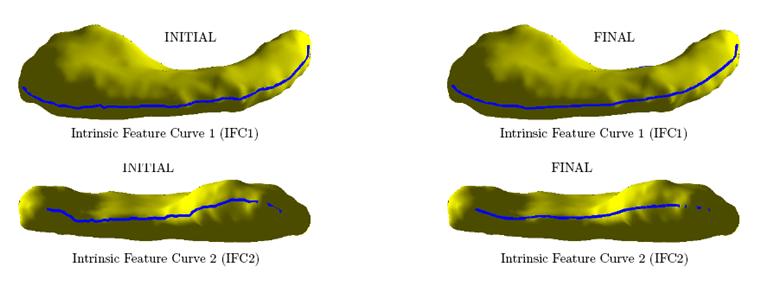
we can easily compute a registration between HC surfaces, called the eigen-harmonic
registration (EHR), which maps eigen-loops to eigen-loops, preserves the
longer intrinsic landmark, and minimizes the harmonic distortion caused by
the azimuthal coordinate. The result is a smooth, one-to-one, feature-matching
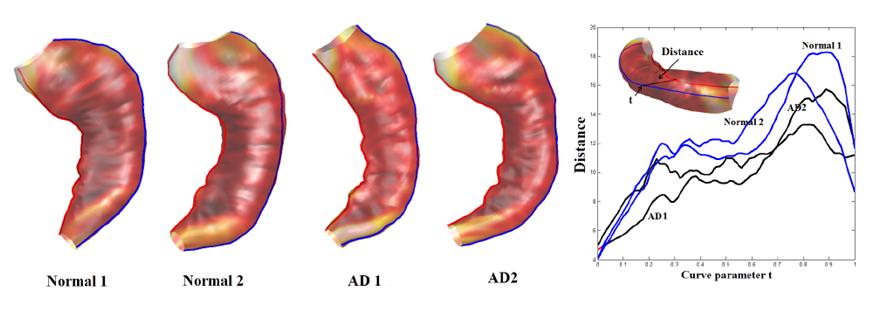
registration with the least distortion. Using EHM and EHR, we can precisely
locate shape changes on HC surfaces and use the algorithm
for shape morphometry on HC surfaces.
Publication:
- Tsz Wai Wong, Lok Ming Lui, Xianfeng Gu, Paul Thompson, Tony Chan and Shing-Tung Yau, Instrinic feature extraction and Hippocampal Surface Registration using Harmonic eigenmap, submitted
Result: