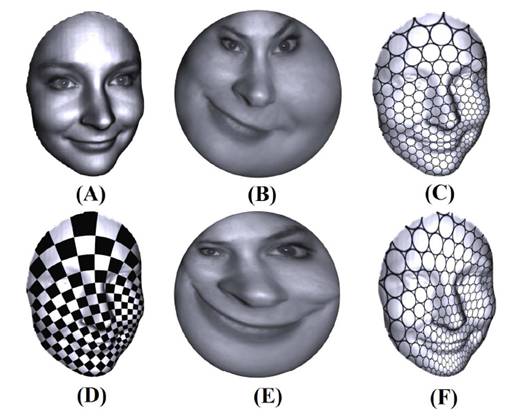
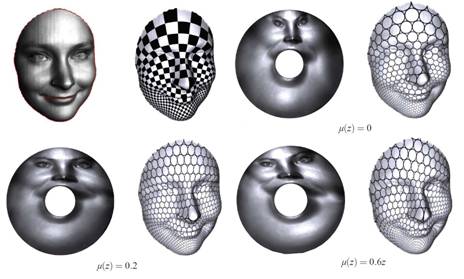
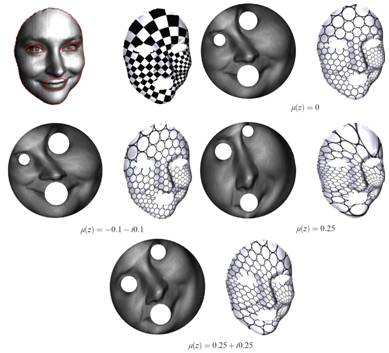
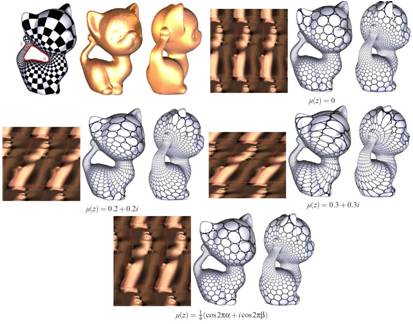
Computation of Quasi-conformal map using
discrete Curvature flow
Project Description:
Surface mapping plays an important role in geometric processing. They
induce both area and angular distortions. If the angular distortion is bounded,
the mapping is called a quasi-conformal mapping. Many surface mappings in
our physical world are quasi-conformal. The angular distortion of a quasi-conformal
map can be represented by the Beltrami differentials. According to quasi-conformal
Teichmuller theory, there is an one to one correspondence between the set
of Beltrami differentials and the set of quasiconformal surface mappings.
Therefore, every quasiconformal surface map can be fully determined by the
Beltrami differentials and can be reconstructed by solving the so-called Beltrami
equation.
In this work, we propose an effective method to solve the Beltrami equation
on general Riemann surfaces.
The solution is a quasi-conformal map associated with the prescribed Beltrami
differential. The main strategy is to define an auxiliary metric of the source
surface, such that the original quasi-conformal map becomes conformal under
the auxiliary metric. The associated map can then be obtained by using the
discrete curvature flow method. In our work, we use both Euclidean and hyperbolic
Yamabe flow for the computation. We tested our algorithm on surfaces scanned
from real life with different topologies. Experimental results demonstrate
the generality and accuracy of our auxiliary metric method.
Publication:
- Wei Zeng, Lok Ming Lui, Xianfeng Gu, Tony Chan and Shing-Tung Yau, Quasiconformal Maps Using Discrete Curvature Flow, submitted