Project Description:
Finding a meaningful 1-1 correspondence between different data, such as images or surface data, has important applications in various fields. It involves the optimization of certain energy functionals over the space of all diffeomorphisms. This type of optimization problems (called the {\it diffeomorphism optimization problems, DOPs}), is especially challenging, since the bijectivity of the mapping has to be ensured. Recently, a method, called the {\it Beltrami holomorphic flow(BHF)}, has been proposed to solve the DOP using quasi-conformal theories. The optimization problem is formulated over the space of Beltrami coefficients(BCs), instead of the space of all diffeomorphisms. BHF iteratively finds a sequence of BCs associated with a sequence of diffeomorphisms, using the gradient descent method, to minimize the energy functional. 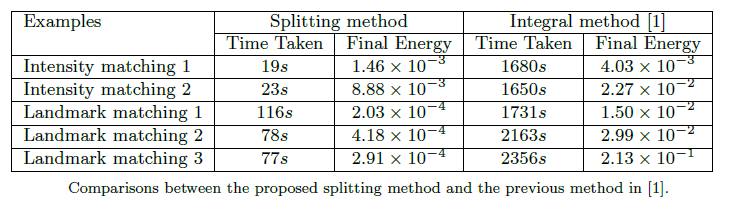The use of BCs effectively controls the smoothness and bijectivity of the mapping, and hence make it easier to handle the constrained optimization problem. However, the algorithm is computationally expensive. 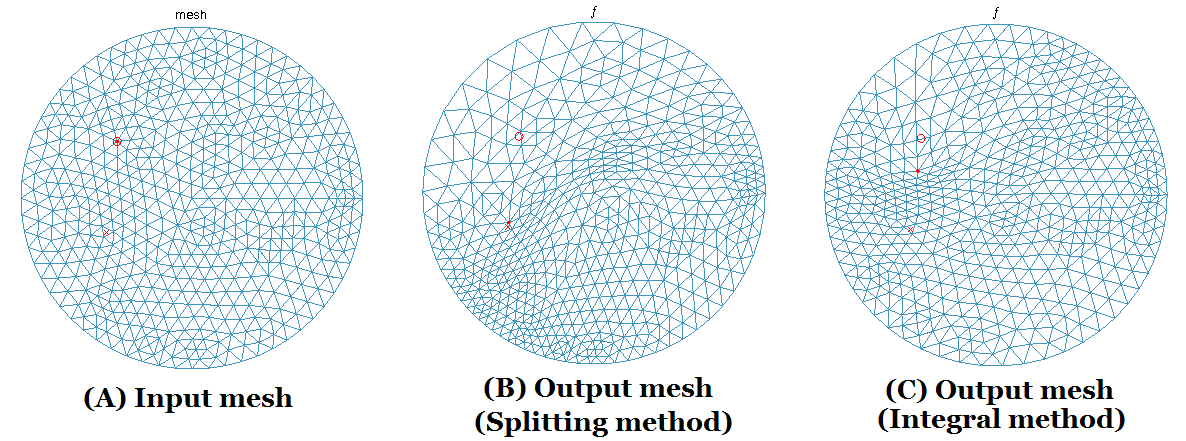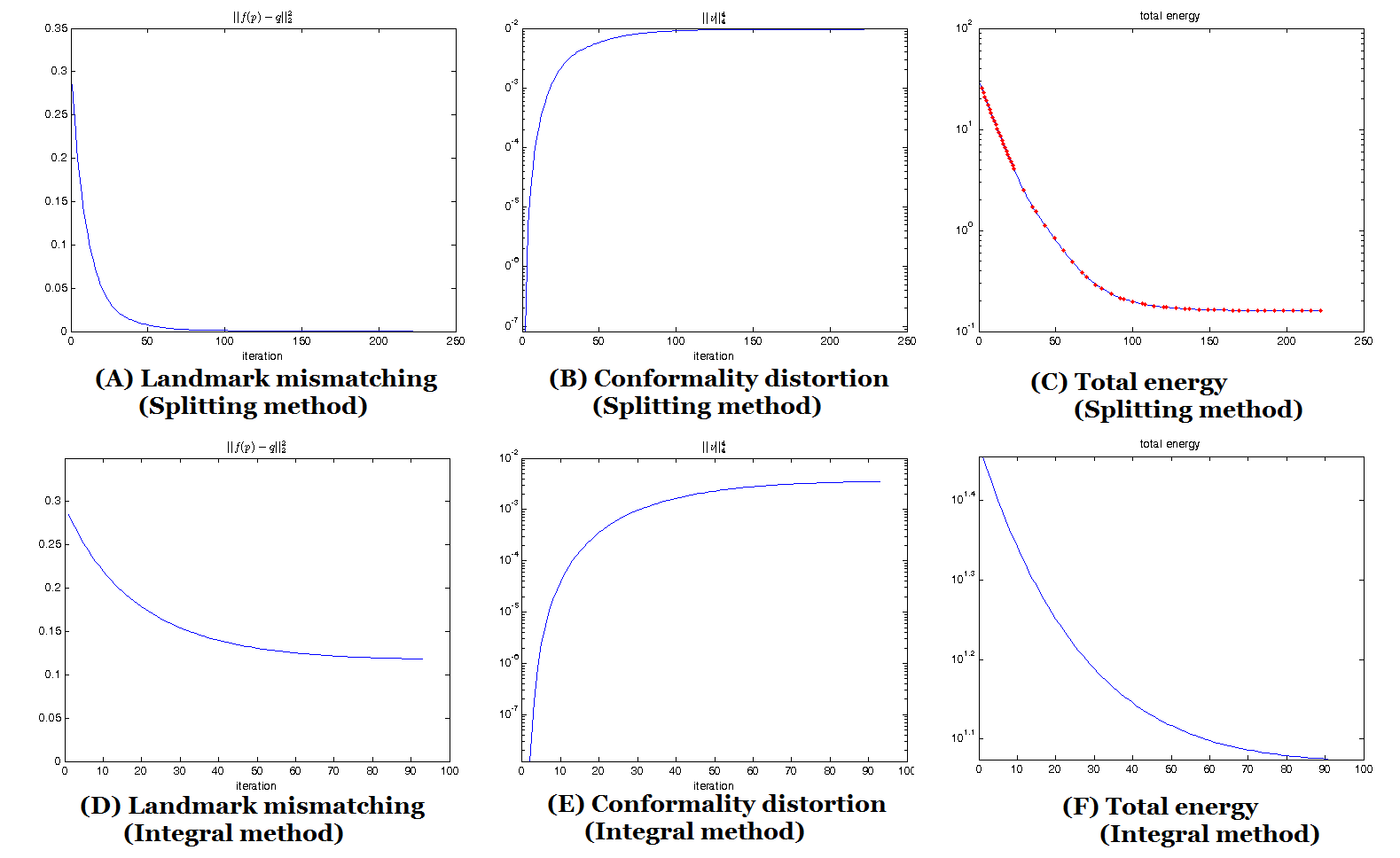In this paper, we propose an efficient splitting algorithm, based on the classical alternating direction method of multiplier (ADMM), to solve the DOP. The basic idea is to split the energy functional into two energy terms: one involves the BC whereas the other involves the quasi-conformal map. Alternating minimization scheme can then be applied to minimize the energy functional. The proposed method significantly speeds up the previous BHF approach. 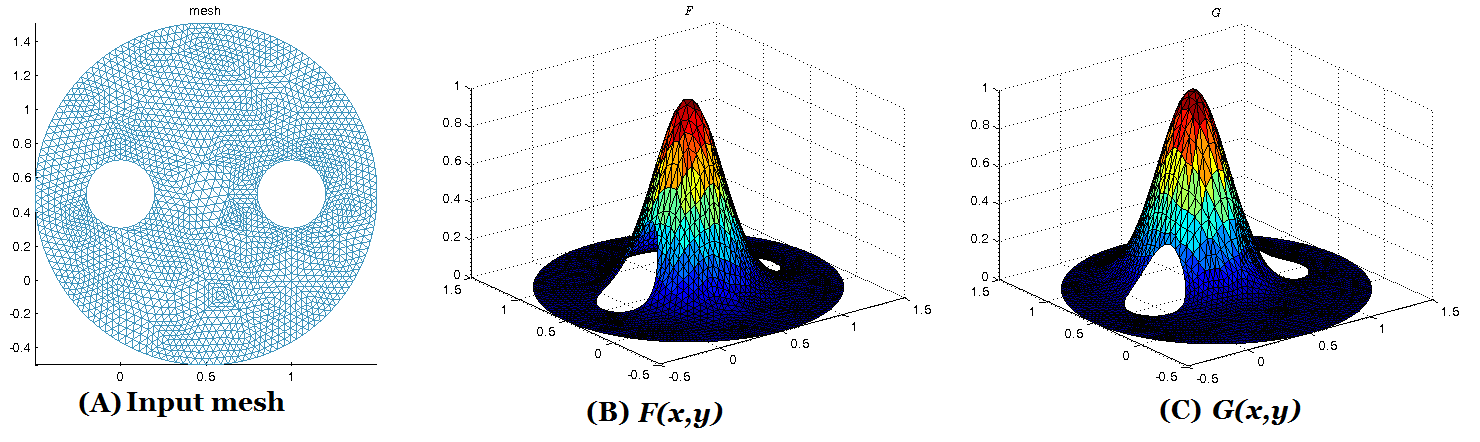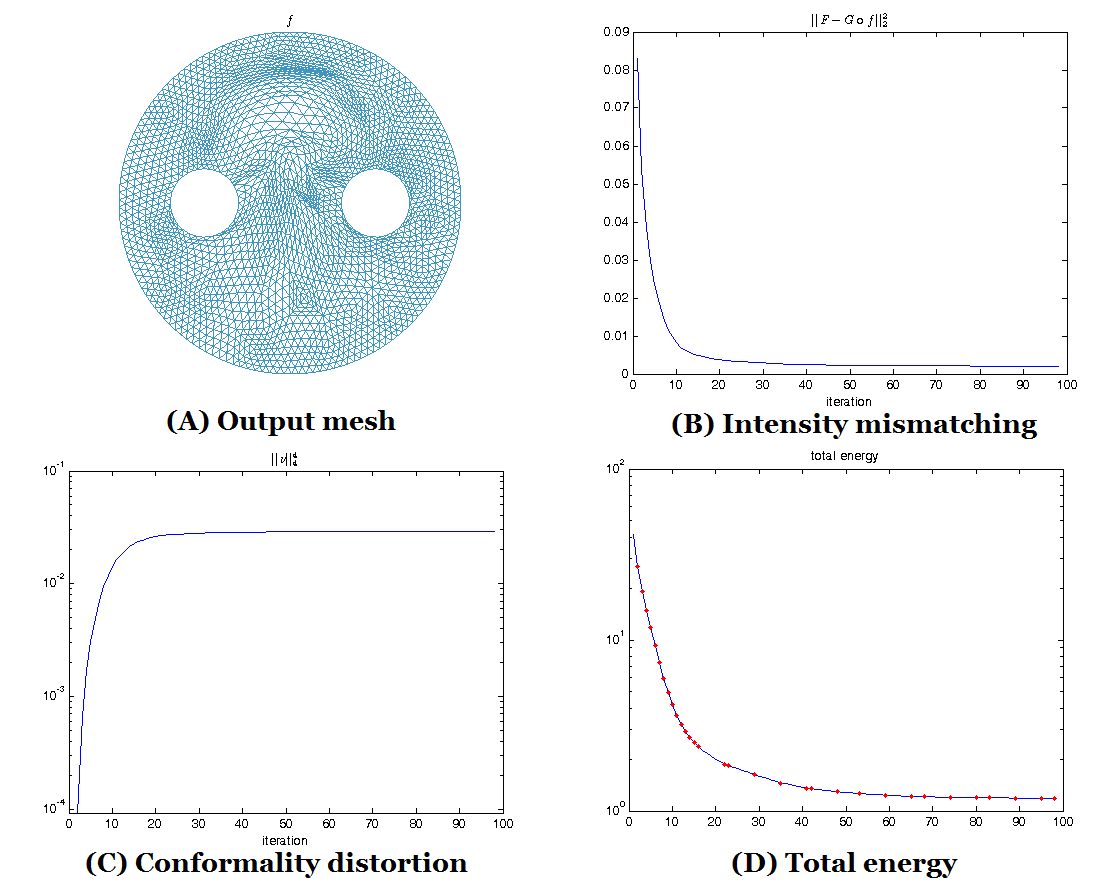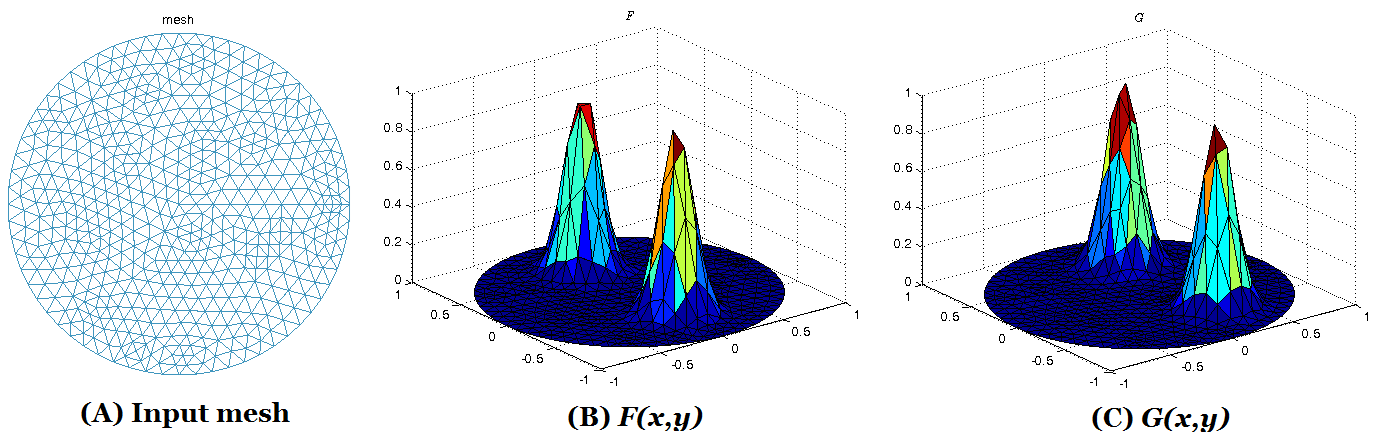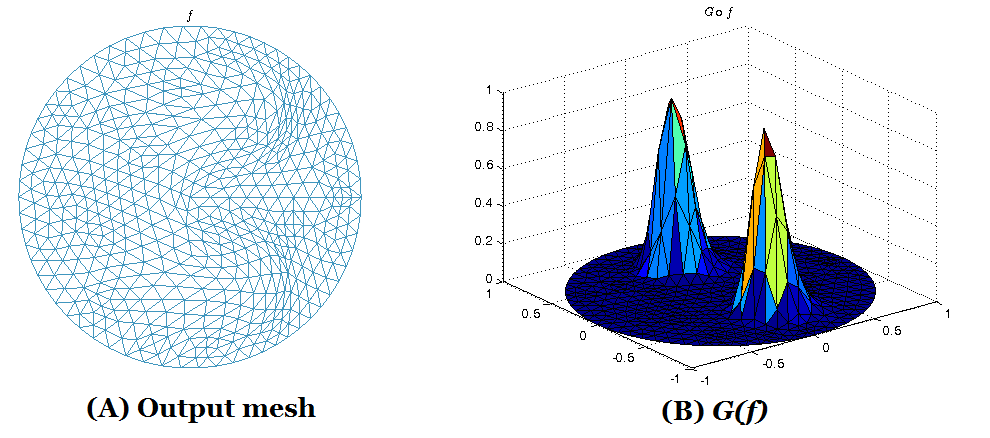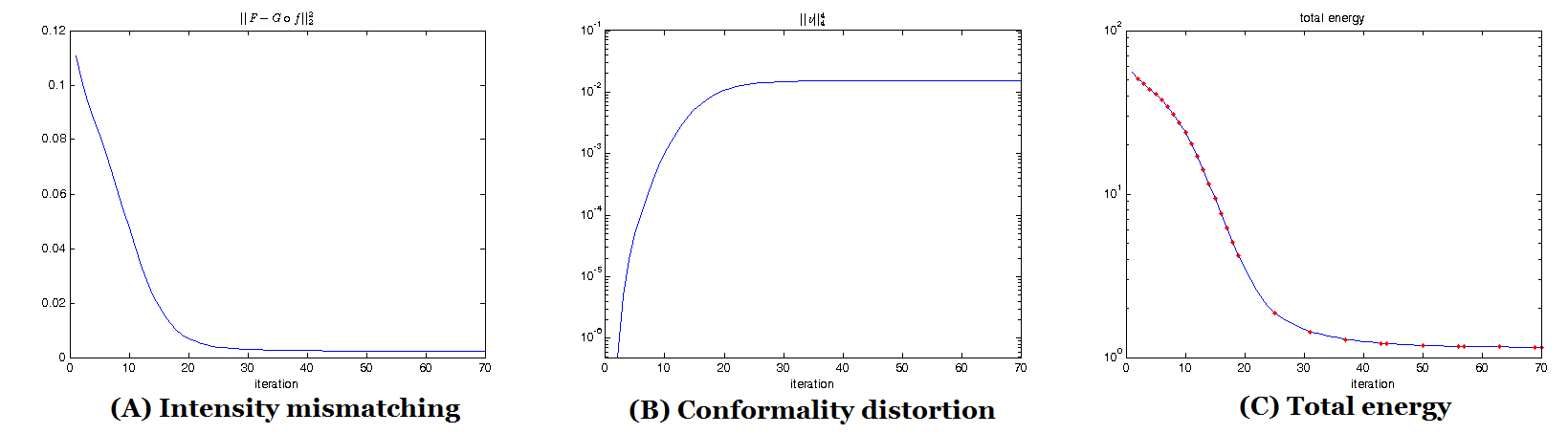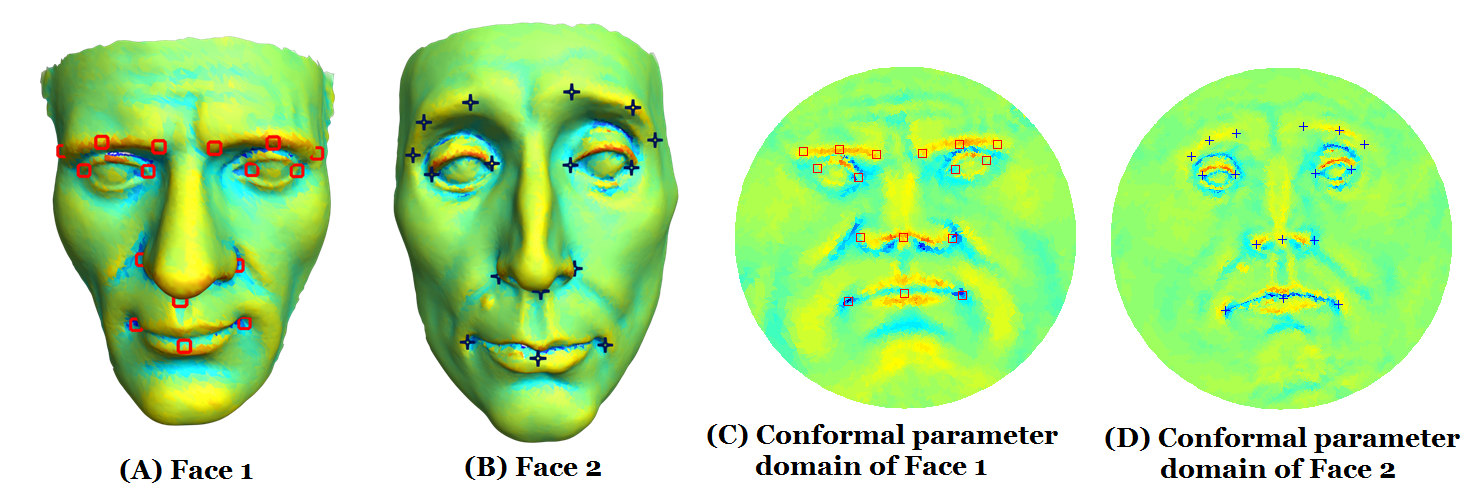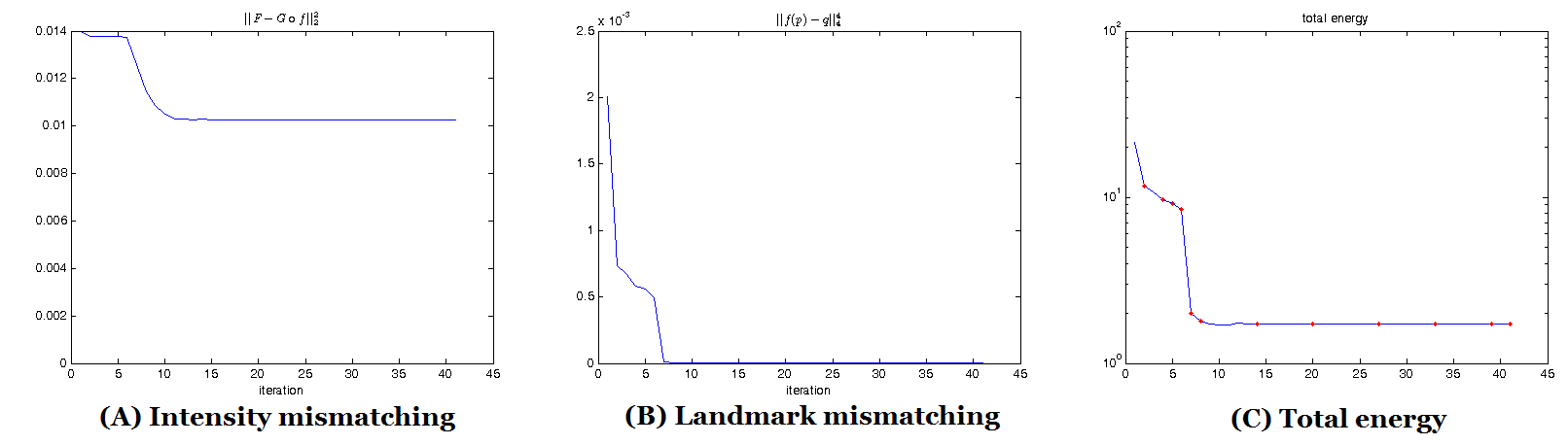It also extends the previous BHF algorithm to Riemann surfaces of arbitrary topologies, such as multiply-connected shapes. Experiments have been carried out on synthetic together with real surface data, which demonstrate the efficiency and efficacy of the proposed algorithm to solve the DOP.

Publication:

• T.C. Ng and L.M. Lui, A Splitting method for Diffeomorphism Optimization Problem using Beltrami coefficients, UCLA CAM Report