Project Description:
We propose a simple representation of bijective surface maps, which helps the process of surface registration. In shape analysis, finding an optimal 1-1 correspondence between surfaces within a large class of admissible bijective mappings is of great importance. Such a process is called surface registration. The difficulty lies in the fact that the space of all surface homeomorphisms is a complicated functional space. Hence, the optimization process over the search space of bijective surface maps becomes challenging. 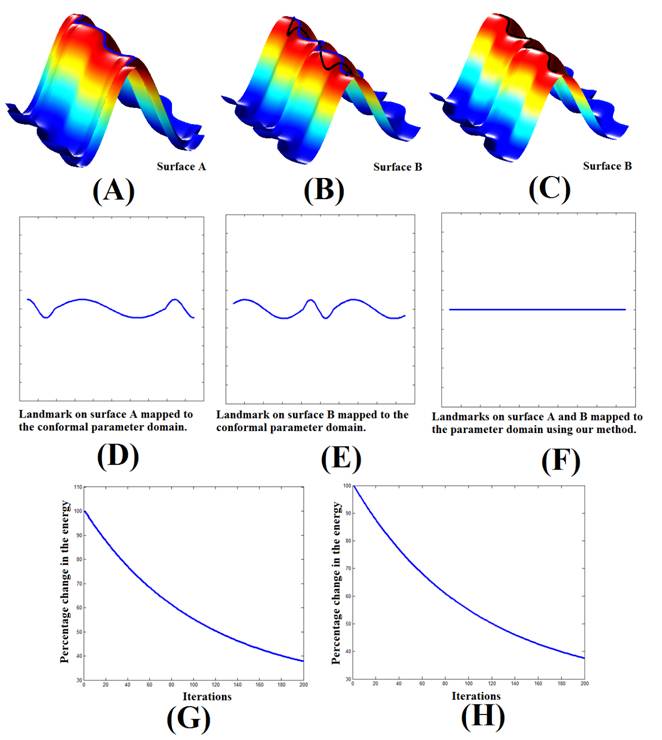To tackle this problem, we propose a novel representation of surface diffeomorphisms using Beltrami coefficients (BCs), which are complex-valued functions defined on surfaces with supreme norm less than 1. Fixing any 3 points on a pair of surfaces, there is a 1-1 correspondence between the set of surface diffeomorphisms between them and the set of Beltrami coefficients on the source domain. Hence, every bijective surface map can be represented by a unique Beltrami coefficient. Conversely, given a Beltrami coefficient, we can reconstruct the unique surface map associated to it using the Beltrami Holomorphic flow (BHF) method introduced in this paper. 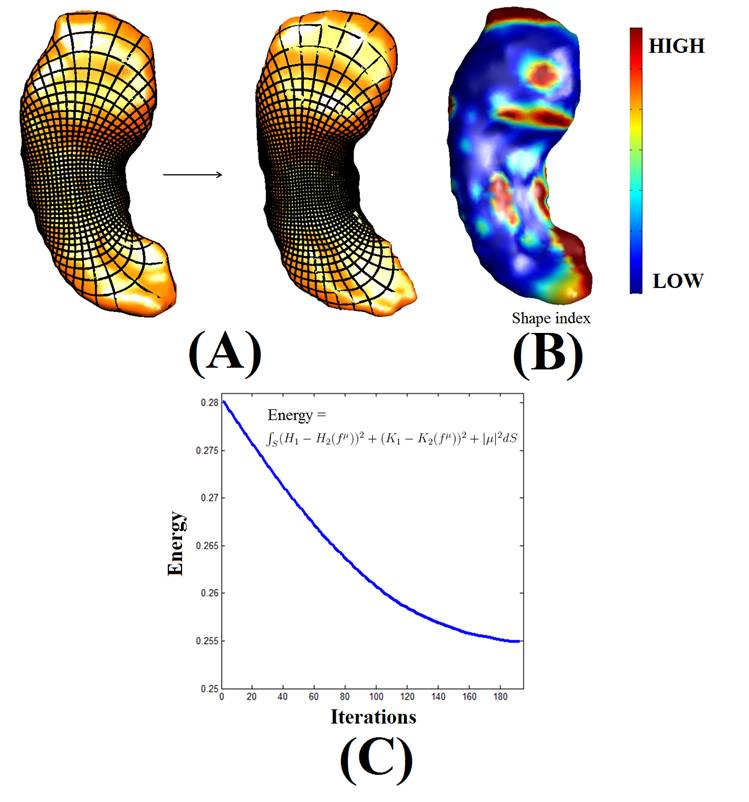Using BCs to represent surface maps is advantageous because it captures most essential features of a surface map. By adjusting BCs, we can adjust the surface homeomorphism accordingly to obtain desired properties of the map. Also, the Beltrami holomorphic flow
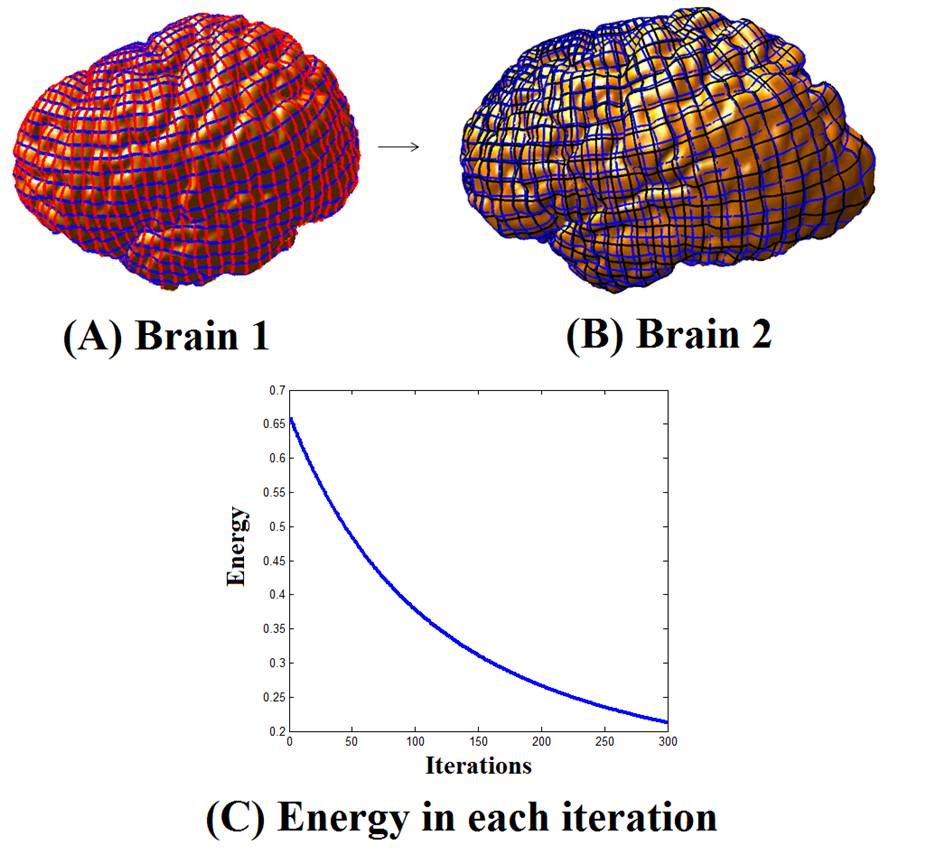
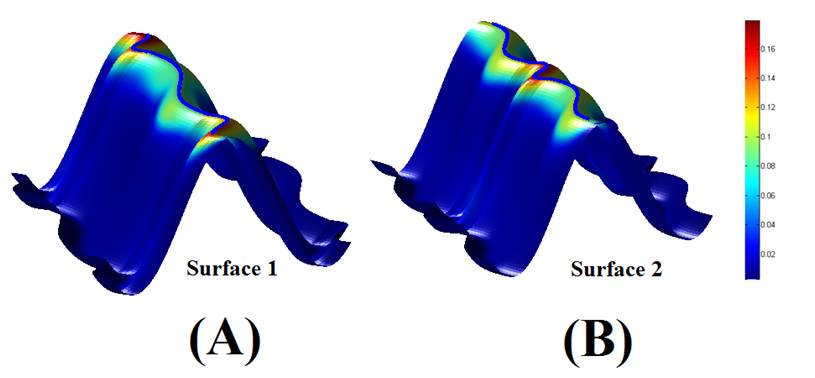
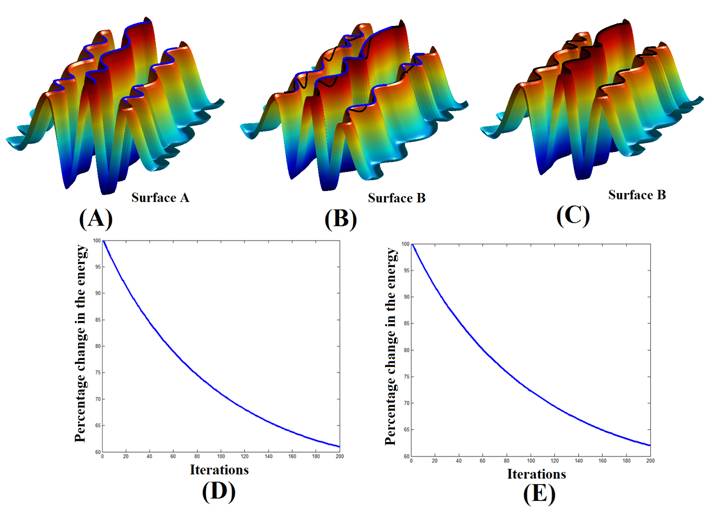
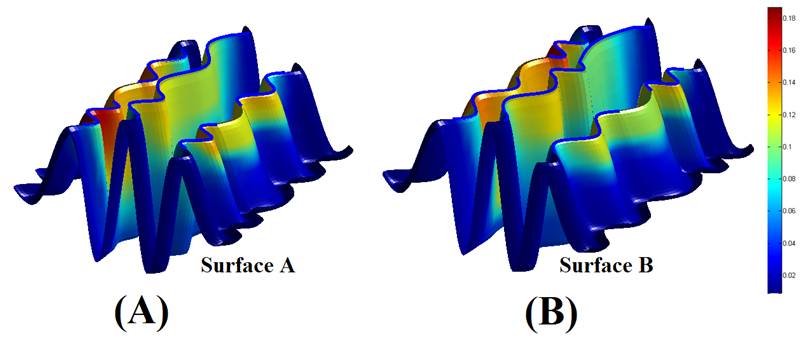
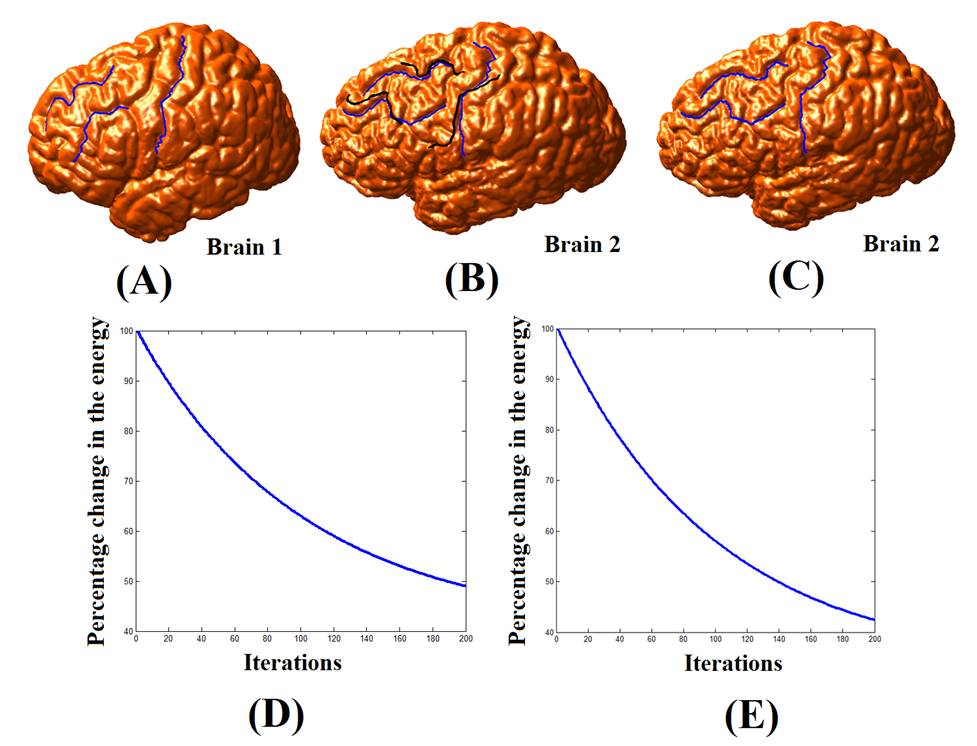
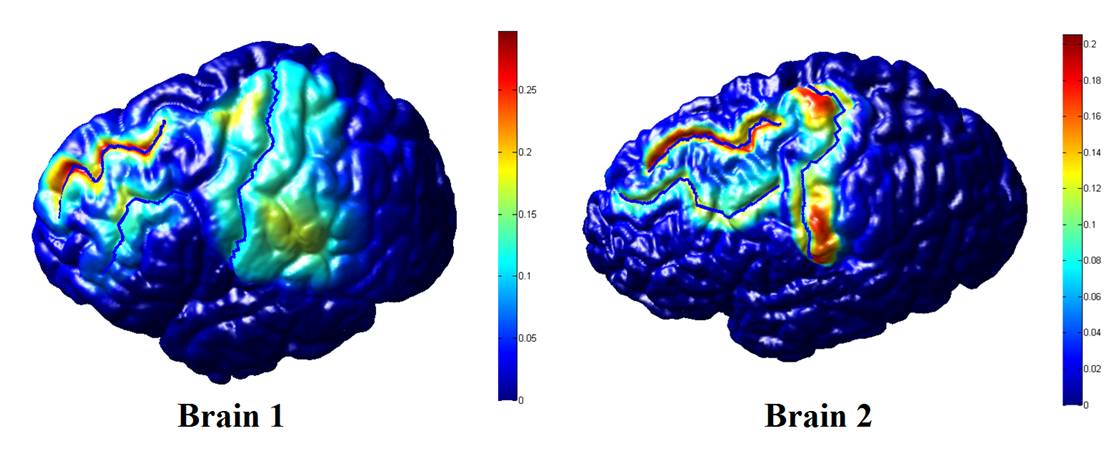
gives us the variation of the associated map under the variation of BC. Using this, variational problems over the space of surface diffeomorphisms can be easily reformulated into variational problems over the space of BCs. The space of BCs is a simple functional space, which makes the minimization procedure much easier. More importantly, a bijective surface map is guaranteed to be obtained during the optimization process. We applied our method to synthetic and real examples, which shows the effectiveness of our proposed method.

Publication:

• Lok Ming Lui, Tsz Wai Wong, Xianfeng Gu, Tony Chan and Shing-Tung Yau, Representation and Property Adjustments of Surface Diffeomorphism using Beltrami Holomorphic Flow, UCLA CAM report 09-19, to be submitted

Result: